
Die Fibonacci-Folge kann mit verschiedenen Algorithmen in Java beschrieben werden. Das interessant ist, wenn man die Zahlen in einem Größenverhältnis setz, erhält man einmal die goldene Spirale, dazu können die Ecken in einer Linie verbunden werden. Da diese häufig in der Natur vorkommt, empfinden wir Objekte/Bilder, die der goldenen Spirale sehr nahe kommen als sehr natürlich.
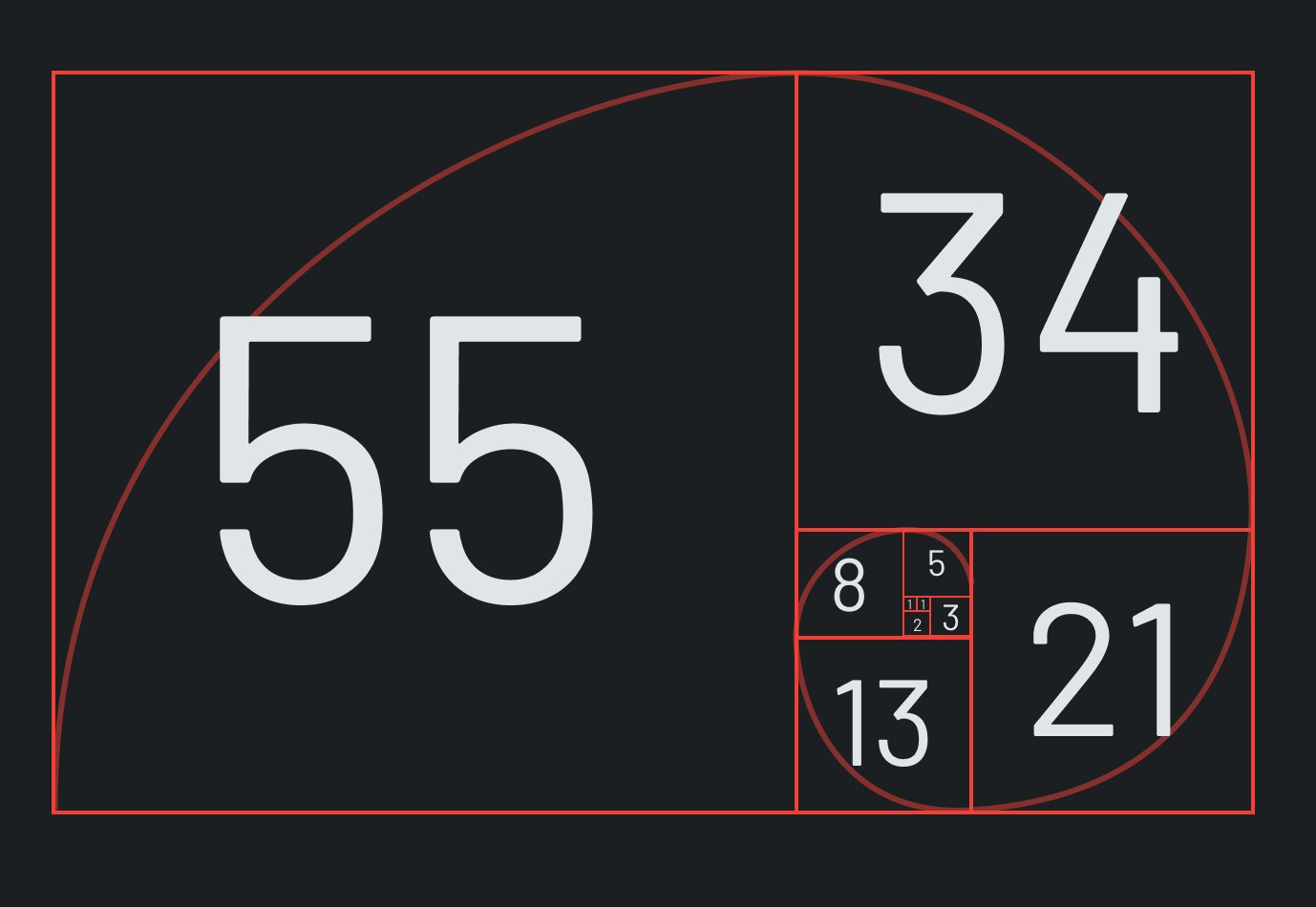
Die Fibonacci-Folge ist eine bekannte Zahlenfolge in der Mathematik, bei der jede Zahl die Summe der beiden vorherigen Zahlen darstellt. Die Folge beginnt normalerweise mit den Zahlen 0 und 1 und lautet: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …
Es ist wichtig zu beachten, dass die Fibonacci-Folge in einer bestimmten Reihenfolge berechnet wird und dass jede Zahl die Summe der beiden vorherigen Zahlen ist. Diese Zahlenfolge wird oft in der Mathematik, Kunst, Architektur und Naturwissenschaften verwendet. Es ist wichtig, die Fibonacci-Folge richtig zu verstehen und anzuwenden, um bestimmte Muster und Strukturen in diesen Bereichen zu erkennen und zu analysieren.
Eine Funktion, die sich selbst aufruft, um Probleme zu lösen, wird als rekursive Funktion bezeichnet. Es ist wichtig, dass eine Abbruchbedingung vorhanden ist, die bestimmt, wann die Funktion nicht mehr aufgerufen wird. Andernfalls resultiert eine unendliche Rekursion und das Programm wird fehlschlagen. Jede Rekursionsebene muss eine Veränderung am Wert durchführen, um die Funktion schließlich beenden zu können.
Wie berechnen wir nun eine Zahl an einer bestimmten Stelle der Fibonacci-Folge? Wir wissen inzwischen, dass eine Fibonacci-Zahl immer die Summer der beiden vorherigen Fibonacci-Zahlen ist. Das bedeutet, wenn wir eine beliebige Zahl, nennen wir sie n, haben, dann wäre das Ergebnis die Summe der beiden vorherigen Zahlen von n. Mathematisch können wir das mit (n - 1) + (n - 2) ausdrücken.
Zusätzlich benötigen wir noch einen Sonderfall für Zahlen, die kleiner als 2 sind, da in der Fibonacci Folge vorausgesetzt wird, dass bei 0 gestartet wird und die 1 folgt. Wenn wir diese Bedingung nicht setzen würde, würden wir negative Zahlen erhalten. Den Fall mit n kleiner 0 habe ich eingeführt, falls jemand eine Negative Zahl in die Methode gibt, da die Fibonacci Folge bei 0 startet, kann nicht bei Werten kleiner als 0 begonnen werden. Genauer gesagt, gibt es keine negative Stelle in der Fibonacci-Folge.
public class Fibonacci {
public static int getFibNumber(int n) throws IllegalArgumentException {
if(n < 0){
throw new IllegalArgumentException("n must be greater than -1");
}
if(n < 2){
return n;
}
return getFibNumber(n - 1) + getFibNumber(n - 2);
}
}Da wir hier allerdings mit dem Datentyp int arbeiten, werden wir bei größerer Zahl rasant einen Overflow erreichen und erhalte falsche Zahlen. Als Beispiel hierführ ein Integer hat eine begrenzte Größe, wie groß also die Zahlen sein können, die dort drinnen gespeichert werden, heißt, wenn das Maximum erreicht wird und +1 rechnet, erhält man den kleinsten möglichen Integer. Dazu das folgende Beispiel, wo wir den Integer mit dem Max Value addieren mit Eins, bedeutet also wir erhalten gar keine Warnung darüber, deshalb ist es wichtig in Java zu wissen, wie groß die Zahlen sein können, die man erhält.
System.out.println(Integer.MAX_VALUE); // 2147483647
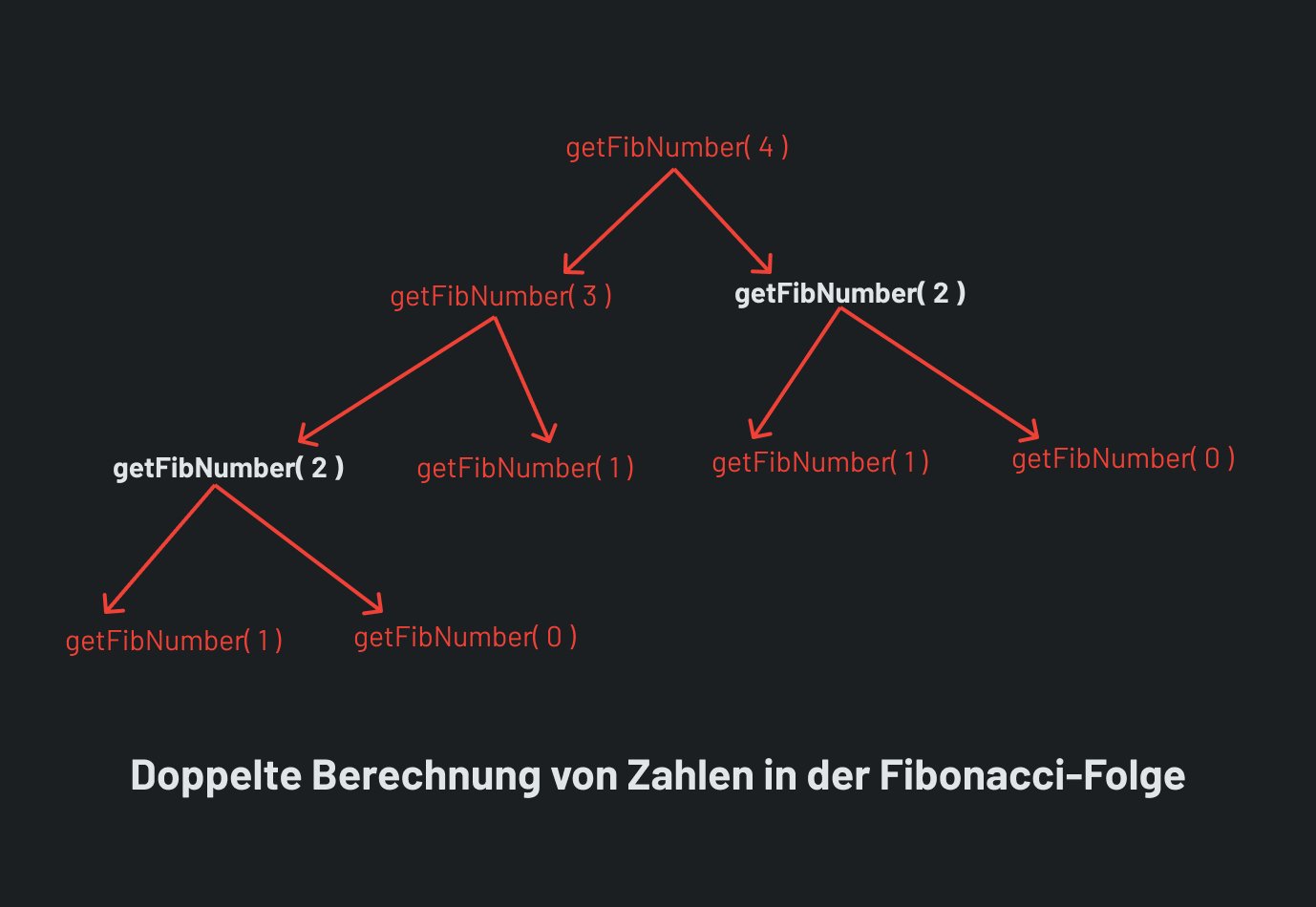
System.out.println(Integer.MAX_VALUE + 1); // -2147483648Ein anderes Problem an dieser sehr einfachen Umsetzung der Programmierung ist, dass Zahlen doppelt berechnet werden, da jedes Mal aufs neue eine Rekursion stattfindet, mit dem Konzept der Memoisation können wir das später verhindern.
In der Grafik kannst du noch einmal sehen, wie hier die 2te Stelle doppelt berechnet werden muss. Um so größere die Stelle in der Fibonacci Folge ist, die wir erhalten wollen, um so häufiger werden sich Berechnungen doppeln, mittels der Memoisation können wir die Ergebnisse speichern und so die Prozesse erheblich beschleunigen.
Bei der oben beschrieben Art von Algorithmus habe ich bereits beschrieben, welche Fehler auftreten können, folgender Code kann zum Beispiel auch die 1000 Fibonacci Zahl in einer rasanten Zeit von um die 2 Sekunden berechnen.
434665576869374564356885276750406258025646605173717804024817290895
36555417949051890403879840079255169295922593080322634775209689
62323987332247116164299644090653318793829896964992851600370447
6137795166849228875
Na, kannst du die Zahl noch aussprechen? Spaß bei Seite, folgende Anpassungen habe ich an unserem Code aus dem ersten Beispiel vorgenommen. Der Datentyp wurde von int auf BigInteger geändert, um auch so große Zahlen wie die 5000 Fibonacci Zahl darstellen zu können. Zusätzlich werden jetzt die bereits erstellten Zahlen zwischengespeichert in der HashMap so muss nicht an jeder stelle neu Rekursive bis zur 0ten stelle alles durchgegangen werden und die Erstellung ist so erheblich schneller.
import java.util.HashMap;
public class Fibonacci {
private static HashMap<BigInteger, BigInteger> store = new HashMap<BigInteger, BigInteger>();
public static BigInteger getFibNumber(BigInteger n) throws IllegalArgumentException {
if (n.doubleValue() < 0) {
throw new IllegalArgumentException("n must be greater than -1");
}
if (n.doubleValue() < 2) {
return n;
}
BigInteger item = store.get(n);
if (item != null) {
return item;
}
BigInteger result = getFibNumber(n.subtract(BigInteger.ONE)).add(getFibNumber(n.subtract(BigInteger.TWO)));
store.put(n, result);
return result;
}
}Im Artikel „Konzept von Memoisation in Python erklärt“ – gebe ich einen detaillierteren Einblick in dieses Konzept zur Beschleunigung der Dinge. Die theoretische Erklärung ist sicherlich auch im Java Kontext interessant.
Ein anderer Fall könnt sein, dass du dir nicht eine spezifische Fibonacci Zahl ausgeben lassen willst, sondern ein Array der Fibonacci-Folge bis zur Hunderterstelle erstellen willst.
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049]
Als Beispiel dafür habe ich nun noch eine Methode geschrieben, die eine ArrayList erstellt, die entsprechende BigInteger verwendet, um auch die größeren Zahlen darstellen zu können.
public static ArrayList<BigInteger> getFibNumbers(int length){
ArrayList<BigInteger> fibNumbers = new ArrayList<BigInteger>();
fibNumbers.add(BigInteger.ZERO);
fibNumbers.add(BigInteger.ONE);
for (int i = 2; i < length; i++) {
fibNumbers.add(fibNumbers.get(i - 1).add(fibNumbers.get(i - 2)));
}
return fibNumbers;
}Als Parameter übergeben wir eine Länge des Arrays, so bekommen wir die Fibonacci Folge bis „length“ und das Ganze in einer Schleife ohne Rekursion.
Zusammenfassend kann man sagen, dass die Fibonacci-Folge ein wichtiger Teil der Mathematik und anderen Bereichen wie Kunst, Architektur und Naturwissenschaften ist. Es ist wichtig, die Fibonacci-Folge richtig zu verstehen und anzuwenden, um bestimmte Muster und Strukturen zu erkennen und zu analysieren. In Java kann man die Fibonacci-Folge mithilfe einer rekursiven Methode berechnen, aber es ist wichtig zu beachten, dass bei großen Zahlen Overflows auftreten können. Dies kann durch die Anwendung der Memoisation verbessert werden, um eine schnellere Berechnung der Fibonacci-Zahlen zu erreichen.
Hinterlasse mir gerne einen Kommentar zum Artikel und wie er dir weitergeholfen hat beziehungsweise, was dir helfen würde das Thema besser zu verstehen. Oder hast du einen Fehler entdeckt, den ich korrigieren sollte? Schreibe mir auch dazu gerne ein Feedback!
Es sind noch keine Kommentare vorhanden? Sei der/die Erste und verfasse einen Kommentar zum Artikel "Java: Fibonacci Folgen - Algorithmen Erklärt"!